Miroslav Beneš, 2001
Informatika I/2/31

Obsah

1. Úvod
2. Základní pojmy
3. Algoritmy
   1. Naivní algoritmus
   2. Knuth-Morris-Prattův algoritmus (KMP)
   3. Boyer-Mooreův algoritmus (BM)
   4. Baeza-Yates-Gonnetův algoritmus (BYG)
   5. Quicksearch
4. Srovnání algoritmů
5. Závěr
6. Literatura

I. Úvod

V dnešní době, kdy se většina dokumentů (ať už na úřadech nebo v běžných podmínkách) vede na počítačích, a tedy v elektronické podobě, je potřeba míti dostatečně silné nástroje k tomu, aby se v daných dokumentech vyhledal nějaký text (slovo, věta apod.) v co nejkratším možném čase. Proto se řadu let vyvíjí různé algoritmy, které tento úkol s odlišnými úspěchy plní.
Tyto algoritmy jsou běžnému uživateli počítače schovány v jiných větších celcích jako jsou různé textové editory, kde je občas nutné nějaké to slovo v textu vyhledat (potažmo zaměnit za jiné). Dalším příkladem mohou být vyhledávací systémy v knihovnách, vyhledávání v databázích, všelijaké vyhledávací servery apod. Principy vyhledávání vzorků v textu se také používají i v jiných oborech než v informatice, příkladem může být například hledání "vzorků" v DNA šroubovici.
Z toho vyplývá, že vyhledávání v textu je poměrně rozsáhlý problém o jehož užitečnosti jistě není sporu. Proto je určitě užitečné uvést si nějaké příklady algoritmů, které tento problém řeší, popsat je a porovnat.

Algoritmy se mohou dělit do několika možných kategorií podle toho za jakým účelem se používají nebo podle svého původu. Můžeme se tedy setkat s algoritmy, které vyhledávají pouze jeden vzorek v daném textu, v jiných případech je možno vyhledávat množinu více vzorků. Rozdíl je také v tom, že některé algoritmy naleznou pouze první výskyt vzorku v textu, jiné naleznou všechny výskyty. Existují algoritmy, které se inspirovaly i jinými obory informatiky jako je např. teorie automatů.

V tomto článku bych se rád věnoval zejména dvěma algoritmům. Prvním je Knuth-Morris-Prattův algoritmus (KMP), druhým je Boyer-Mooreův algoritmus (BM). Společným rysem obou je skutečnost, že vyhledávají všechny výskyty jednoho vzorku v daném textu. Na KMP se dá nahlížet jako na upravený konečný (v tomto případě vyhledávací) automat. BM se na druhou stranu jeví jako naivní vyhledávací algoritmus (viz dále) se dvěmi důležitými heuristikami.
Představitelem skupiny algoritmů, které vyhledávají celou množinu vzorků je např. algoritmus Aho-Corasickové, který je založen na poznatcích právě z teorie automatů.
V dalším odstavci bych rád zmínil další dva zajímavé a relativně nové algoritmy: Baeza-Yates-Gonnet, který je založen na vyhledávání pomocí bitových masek, a algoritmus Quicksearch, jehož autorem je D.M. Sunday.

Nejprve si však zaveďme několik důležitých pojmů a definic, které se budou hodit k pozdějšímu popisu a zkoumání algoritmů.

>>>Obsah

II. Základní pojmy

I přesto, že většina lidí v principu chápe, co vyhledávání v textu je, definujme si tento pojem alespoň trochu přesněji a formálněji.
Nejprve si vysvětlíme některé základní pojmy potřebné pro popis daného problému. Abecedou Σ rozumíme konečnou množinu znaků. Například Σ={0,1} nebo Σ={a,b,...,z}. Prvky této množiny se často nazývají znaky, písmena nebo symboly. Slovem v abecedě Σ je míněna konečná posloupnost znaků z této abecedy. Prázdným slovem se rozumí posloupnost délky 0 a obvykle se značí ε (ε nepatří do Σ).
Množina všech slov v abecedě Σ se značí Σ^*. Na této množině je definována operace skládání (konkatenace), která dvěma slovům x a y délek m a n přiřadí slovo xy délky m+n. Tato operace je asociativní (to znamená, že (xy)z je to samé slovo jako x(yz)) a pro více než jednoprvkovou abecedu nekomutativní (v případě jednoprvkové abecedy: aa"=" aa, pokud Σ ={a}; v případě víceprvkové např. xy není rovno yx pro x, y navzájem různá). Roli jednotkového prvku této operace hraje prázdné slovo ε, tedy xε=εx=x pro každé x z ε.
Nechť x je prvkem Σ^*. Potom délkou slova x rozumíme počet znaků v x. Zapisujeme |x|. Tedy jak bylo poznamenáno |ε|=0.
Řekneme, že slovo x z Σ^* je předponou (prefixem) slova y z Σ^*, existuje-li takové slovo u z Σ^*, že xu=y. Takové u zřejmě existuje nejvýše jedno a je-li neprázdné, říkáme, že x vlastní předpona. Obdobně, řekneme, že slovo x z Σ^* je příponou (suffixem) slova y z Σ^*, existuje-li takové slovo v z Σ^*, že vx=y. Opět takové v existuje nejvýše jedno a je-li neprázdné, mluvíme o vlastní příponě. Zřejmě platí, že ε je vlastní příponou a předponou každého slova z Σ^*. Podobně každé slovo je svou jedinou nevlastní příponou i předponou.
Pro příklad si uveďme, že slovo ab je předponou slova abbdad a to předponou vlastní. Zároveň je vlastní příponou slova abbab.
Pro další účely si zaveďme ještě jeden jednoduchý pojem, prefix o k znacích. Prefix vzorku P[1..m] o k znacích, tedy P[1..k], budeme značit Pk. Podobně budeme mít tento pojem i pro prohledávaný text (Tk).
Nyní se vraťme k formulaci problému vyhledávání v textu. Nechť máme danou abecedu Σ a tím i množinu Σ^*. Předpokládejme, že máme dány dva textové řetězce (nejlepší je představit si je jako pole jednotlivých znaků). Řetězec P = p1...pm (nebo jako pole znaků P[1..m]) budeme nazývat vzorek. Jeho délka je m. Řetězec T = t1...tn (T[1..n]) bude prohledávaný text délky n. Oba řetězce jsou slova z Σ^*.
Říkáme, že vzorek P se v textu T nachází s posunutím s (jinými slovy řečeno, nachází se v textu T na pozici s+1), jestliže 0<=s<=n-m a zároveň T[s+1..s+m]=P[1..m] (pro všechna j 1<=j<=m ts+j=pj). Pokud se vzorek P v prohledávaném textu T nachází nazýváme s platným posunem . Jinak je tento posun neplatný. Problém vyhledávání jednoho vzorku v textu lze tedy formulovat jako problém nalezení všech platných posunů, se kterými se vzorek P nachází v textu T.

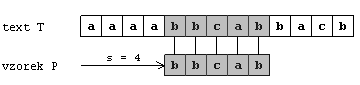
Tento obrázek znázorňuje předchozí definici o vyhledávání v textu. Vzorek P=bbcab se nachází v textu T s platným posunem 4, neboli na 5. pozici.

>>>Obsah

III. Algoritmy

Po vysvětlení všech potřebných pojmů a formulaci daného problému se můžeme začít zabývat jednotlivými algoritmy. Nejprve se zlehka podíváme na naivní vyhledávací algoritmus a jeho časovou složitost, aby se určitým způsobem zdůvodnila potřeba lepších a efektivnějších vyhledávacích algoritmů. Poté probereme již zmíněné dva algoritmy (Knuth-Morris-Pratt a Boyer-Moore).

1. Naivní algoritmus

Tento algoritmus je v podstatě výsledkem první myšlenky, která každého napadne, když dostane za úkol navrhnout algoritmus na vyhledávání v textu. Jednoduše řečeno spočívá v prozkoumání všech možností (ne tedy doslova, ale v principu ano). Jak tomu u takových algoritmů bývá, jeho časová složitost není příliš dobrá.
Myšlenka je jednoduchá. Budeme procházet zadaný text a na každé pozici zkontrolujeme, zda tu nezačíná daný vzorek. Princip znázorňuje následující obrázek.

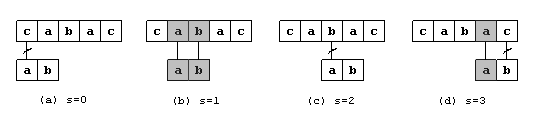
Jak je z obrázku vidno, vzorek se jakoby postupně posouvá pod daným textem a na každém místě se kontroluje, zda se zde nenachází příslušný vzorek. V tomto příkladu byl vzorek nalezen na druhé pozici (s posunem 1, případ (b)). V ostatních případech vždy nastala na určitém místě vzorku kolize.
Neefektivnost tohoto algoritmu spočívá právě ve skutečnosti, že pokud narazím na neshodu, posunu vzorek pouze o jedno místo doprava a začnu porovnávat znovu, a to až do konce prohledávaného textu. Tímto postupem se tedy nevyužívají informace, které byly získány v předchozím kroku. Například u našeho obrázku po tom, co jsem našel vzorek v případě (b), nemusím kontrolovat pozici o jednu vpravo, ale mohu přistoupit až k nákresu pod písmenem (d).
Tyto informace, které závisí právě na zadaném vzorku se snaží využívat efektivnější algoritmy, které si zde ukážeme.
Naivní algoritmus by v pseudokódu mohl vypadat asi následovně:

  (1)  n = length(T)
  (2)  m = length(P)
  (3)  for s = 1 to n-m+1
  (4)   if T[s..s+m-1] == P[1..m]
  (5)    then print("Vzorek se nachází na pozici", s)

Nyní se kód rozeberme a podívejme se na časovou složitost algoritmu. První dvě řádky obstarávají pouze uložení délky obou textových řetězců do proměnných n a m. Posouvání vzorku pod textem zajišťuje cyklus, který začíná na řádce (3). Provede se přesně (n-m+1)-krát, což je počet pozic, na kterých se může vzorek vyskytovat. Řádka (5) jen informuje o nalezení vzorku v textu. Pro určení časové složitosti je klíčová řádka číslo 4. Zde se provádí porovnávání vzorku s daným textem. Tento pseudozápis může ve skutečnosti být while cyklus, který porovnává jednotlivé znaky dokud nenarazí na neshodu nebo na konec vzorku, v tomto případě se vykoná řádka (5). Je snadné nahlédnout, že v nejhorším případě (to je že vždy projdu všechny znaky ve vzorku) se while cyklus provede m-krát. Časová složitost v nejhorším případě je tedy O((n-m+1)*m).

>>>Obsah

2. Knuth-Morris-Prattův algoritmus (KMP)

Mezi prvními, kteří si uvědomili, že informace, které získává naivní algoritmus svým porovnáváním znak po znaku, mohou být velmi cenné pro návrh efektivního algoritmu, byl právě Knuth se svými společníky Morrisem a Prattem. Jejich nápad spočíval v tom, že pokud se tyto informace využijí správným způsobem, může se vzorek nad prohledávaným textem posouvat i o více než pouze o jeden znak doprava. Tím se významně zkrátí doba potřebná k prohledání textu. Také je zbytečné se v prohledávaném textu vracet ke znakům, které již byly analyzovány tak jak to činí naivní algoritmus. Toto vracení spočívá ve skutečnosti, že pokud při porovnávání vzorku s daným textem narazím na neshodu, vrátím se zpět na začátek vzorku a ten posunu o jedno místo doprava. Tato činnost je zřejmě zbytečná, neboť já již mám informaci o předchozích znacích, stačí ji pouze dostatečně využít. Vracení se v textu může přinést i další problém, který není na první pohled zřejmý. Při zpracovávání delšího textu, určitě není tento text v paměti počítače celý. Ze souboru se načítá po kusech do nějakého bufferu v paměti, se kterým se poté pracuje. Podívejme se na následující příklad.

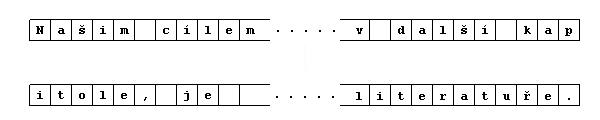
Dejme tomu, že v takovémto textu hledáme výskyt slova kapka. Dva řádky v obrázku představují dva kusy textu tak, jak jsou načteny do paměti (bufferu). Naivní algoritmus prochází prvním bufferem a na konci s podezřením, že se nachází uprostřed vzorku načte nový kus textu a tento zahodí. Ovšem hned u prvního znaku zjistí neshodu a vzhledem ke své funkci mu nezbude nic jiného než se v textu vrátit. To ale představuje další přístup na disk, neboť se musí načíst předchozí kus textu. Princip algoritmu KMP zajistí, že se nic takového nestane.

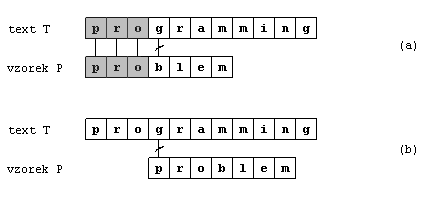
Tento obrázek je příkladem výpočtu KMP algoritmu. Porovnávání vzorku s textem začíná jako obvykle u prvního znaku zleva (vzorek je zarovnán s textem). Algoritmus postupuje dokud nenarazí na neshodu na čtvrté pozici mezi znaky b a g (obrázek (a)). Z předchozích znaků okamžitě víme, že posun vzorku o jeden nebo dva znaky nemá význam. Posun o tři znaky ale může splnit účel. Tím se vzorek zarovná s textem nad znakem, kde nastala neshoda. Odtud dále může pokračovat porovnávání. Jak vidno na této pozici se hned první písmeno vzorku neshoduje se znakem v textu (obrázek (b)), vzorek se poté posune o jedno místo doprava. Velikost takového posunu (o tři v prvním nebo o jeden znak v dalších případech) závisí pouze na charakteru a formě každého vzorku. Posun je nezávislý na prohledávaném textu. Jeho velikost určuje tzv. prefixová funkce.
Díky prefixové funkci si před spuštěním vlastního vyhledávacího algoritmu předpočtu hodnoty posunů pro jednotlivé pozice ve vzorku do nějaké tabulky. Mnoho efektivních vyhledávacích algoritmů používá podobné předpočítané tabulky, které se později v průběhu vyhledávání používají. Tedy jak je patrné algoritmus KMP bude mít dvě fáze. V první fázi si z daného vzorku vypočítáme potřebné hodnoty posunů. Druhá fáze bude uskutečňovat vlastní vyhledávání.
Nejdříve se tedy věnujme první fázi a prefixové funkci. Tato funkce vyjadřuje chování vzorku vzhledem k posunům k sobě samému. Uveďme si ještě jeden příklad.

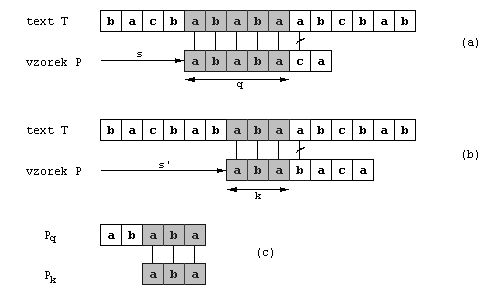
Na obrázku (a) vidíme, že při takovémto zarovnání (s posunem s), se prvních pět písmen vzorku shoduje s pěti písmeny v textu (q=5), přičemž na znaku šestém došlo k neshodě. Z informace, že pět písmen se shodovalo, můžeme okamžitě vyvodit, které to byly, neboť je to prvních pět písmen ve vzorku, a také můžeme zjistit příslušný posun. Je možné určit posuny, o kterých již teď mohu prohlásit, že jsou neplatné, a tím je v budoucnu přeskočit. Zde je na první pohled jasné, že posun o jedno políčko doprava (tedy posun s+1) je neplatný, neboť první písmeno ve vzorku (a) by bylo zarovnáno k písmenu v textu, o kterém již máme informaci, že se shodovalo s druhým písmenem ve vzorku (b). Posun s+2 na obrázku (b) naopak dává jistou naději, že by vzorek mohl být nalezen na tomto místě, neboť tři znaky se shodují.
K navržení kódu, který vypočítá dané hodnoty je tedy třeba vyřešit následující problém. Nechť máme dány znaky P[1..q], o kterých víme, že se shodují s těmito znaky v textu T[s+1..s+q] (v našem příkladu je to slovo ababa, na obrázku vybarvená políčka). Jaký je nejmenší posun s'>s takový, aby platilo P[1..k]=T[s'+1..s'+k], přičemž s'+k=s+q. Slovy řečeno to znamená přesně to, o co se snažíme. Jak moc můžeme vzorek posunout doprava tak, aby se předpona vzorku kratší než počet znaků (ababa), které se předtím shodovaly (ababa, tedy 5), shodovala s příponou slova v textu (ababa), které bylo středem shody (ababa). Pokud taková předpona není (k=0) posuneme vzorek o počet znaků, které se shodovaly (q=5).
Tedy posun s' je nejmenší takový, že je větší než s a není nezbytně neplatný. Jak bylo řečeno v nejlepším případě je nový posun s' roven s+q. V každém případě již nemusíme porovnávat prvních k znaků vzorku, neboť jejich shodu v textem máme zaručenou.
Tyto informace se dají spočítat porovnáváním vzorku se sebou samým, jak je hrubě naznačeno na obrázku (c). Víme, že T[s'+1..s'+k] (ababa) je část známého textu, a tedy to musí být přípona jisté části P, která také byla prozkoumána. Je to přesně přípona Pq. Nyní můžeme přesně formulovat požadavek na posun s' a to pro každou pozici ve vzorku.
Nechť mám vzorek P[1..m], potom prefixová funkce (udává posuny s') vypadá následovně:

  π : {1,...,m} -> {0,...,m-1}, taková že

    π[q]= max{k: k<q and Pk je příponou Pq}.

Pro prefixovou funkci dále platí, že pro každé q z {1,...,m} je π[q]<q.

Pozn. π[q] tedy představuje délku nejdelší předpony P, která je příponou Pq.

Nyní se podívejme, jak bude algoritmus KMP fungovat jako celek. Tedy první fází je výpočet prefixové funkce, který jsme si v principu popsali. Následuje fáze druhá, vyhledávání. Princip je velice jednoduchý. Na začátku zarovnám vzorek vůči textu a začnu porovnávat. Pokud narazím na neshodu, podívám se do tabulky prefixové funkce s indexem, který odpovídá pozici ve vzorku, kde došlo k neshodě. S tabulky zjistím číslo, které udává znak vzorku (číslo určuje jeho pozici ve vzorku) který se, když příslušně zarovnám vzorek k textu, bude nacházet přesně nad znakem v textu, který byl příčinou neshody (vzorek se tedy posune doprava). Vzorek budu tímto způsobem posouvat doprava dokud nenarazím na jeho začátek nebo nebudu moci pokračovat od dané pozice dalším porovnáváním. Takto pokračuji dokud nenarazím na konec textu. Pokud vzorek v textu najdu, oznámím to a pokračuji dále (dá se totiž uvažovat, že u posledního znaku ve vzorku došlo k neshodě).
Nyní si již můžeme uvést zápis algoritmu v pseudokódu (na vstupu je text T a vzorek P).

  (1)  n = length(T)
  (2)  m = length(P)
  (3)  π = Prefix_func(P)
  (4)  q = 0
  (5)  for i = 1 to n
  (6)    while (q > 0 && P[q+1] != T[i]) q = π[q]
  (7)    if P[q+1] == T[i] then q = q+1
  (8)    if q = m then 
  (9)      print("Vzorek se nachází na pozici", i-m+1)
 (10)      q = π[q]

Prefix_func(P)
  (1)  m = length(P)
  (2)  π[1] = 0
  (3)  k = 0
  (4)  for q = 2 to m
  (5)    while (k > 0 && P[k+1] != P[q]) k = π[k]
  (6)    if P[k+1] == P[q] then k = k+1
  (7)    π[q] = k
  (8)  return π

Nyní si určíme časovou složitost algoritmu. Nejprve výpočet prefixové funkce. Základem je, že vnitřní while cyklus se provede nejvýše tolikrát jako cyklus vnější. Platí totiž, že každým průchodem vnitřním cyklem se proměnná k sníží, neboť π[k]<k. Současně se proměnná k může zvýšit nejvýše jednou v každém kroku vnějšího cyklu (díky řádce (6)). Z toho evidentně plyne, že počet průběhů vnitřním cyklem je menší roven počtu kroků vnějšího cyklu. Odtud již plyne, že časová složitost výpočtu prefixové funkce je O(m).
Obdobnou úvahou dojdeme k tomu, že časová složitost vyhledávací fáze je O(n). Časová složitost celého algoritmu je tedy O(m+n), což je výrazně lepší než u naivního algoritmu.

V úvodu celého referátu bylo řečeno, že KMP algoritmus do jisté míry souvisí s konečnými automaty. Jak? Je to velice jednoduché. Předpokládejme, že máme vzorek P délky m. Definujeme si tedy konečný automat, který bude mít m+1 stavů. Přechody mezi jednotlivými stavy budou postupně určené jednotlivými písmeny vzorku. Tedy např. přechod mezi nultým a prvním stavem bude podle písmena p1, přechod mezi prvním a druhým stavem podle p2 atd. Zbylé přechody (tedy jakési chybové) bude určovat právě prefixová funkce. Vstupním stavem bude stav 0 a výstupním stav m. Samotné vyhledávání bude realizováno jako práce takového automatu se vstupem, který odpovídá zadanámu textu. Je zde pouze rozdíl v tom, že pokud se pomocí prefixové funkce vrátím do některého předešlého stavu, okamžitě zkusím přes to samé písmeno (které vlastně způsobilo neshodu) přejít do následujícího stavu, jinak se vracím dále.
Uveďme si příklad.

Na obrázku je konečný automat pro vzorek perpetrate. Nyní si ukážeme, jak bude vypadat výpočet automatu pro dvě různá slova. Výpočet je znázorněn jako posloupnost stavů, mezi kterými jsou písmena, přes která se mezi stavy přechází.

(a) budeme prohledávat text perperpetrate:      0^p1^e2^r3^p4^e5^r2^r 3^p4^e5^t6^r7^a8^t9^e10
(b) nyní to bude text perpespetrate:      0^p1^e2^r3^p4^e5^s2^s 0^p1^e2^r3^p4^e5^t6^r 7^a8^t9^e10

>>>Obsah

V této kapitole si předvedeme další chytrý a efektivní algoritmus jehož autory jsou S. Boyer a J. Strother Moore. Jak bylo řečeno v úvodu, tento algoritmus se příliš zásadně neliší od naivního algoritmu, který jsme si ukázali. Je zde pouze několik odlišností. Abychom si je ukázali, předvedeme si ihned, jak Boyer-Mooreův algoritmus vypadá. Na vstupu je text T, vzorek P a abeceda Σ.

  (1)  n = length(T)
  (2)  m = length(P)
  (3)  λ = Last_Occur_func(P,m,Σ)
  (4)  γ = Good_suff_func(P,m)
  (5)  s = 0
  (6)  while (s <= n-m)
  (7)    j = m
  (8)    while (j > 0 && P[j] == T[s+j]) j = j-1
  (9)    if j == 0 
 (10)      then print("Vzorek se nachází na pozici", s+1)
 (11)           s = s+γ[0]
 (12)      else s = s+max(γ[j], j-λ[T[s+j]])

V čem se tedy tento algoritmus podobá a v čem se liší od naivního algoritmu? Podobnost je jak ve struktuře (což zas tak podstatné není) tak ve skutečnosti, že se vzorek opět porovnává s daným textem a v případě neshody se vzorek posune doprava. Odlišnosti jsou v tom, že vzorek se s textem porovnává zprava doleva, tedy odzadu (u naivního algoritmu se porovnávání provádí zleva doprava). Pokud narazím na začátek vzorku, je jasné že jsem v textu našel jeho výskyt. Zde je další rozdíl, neboť při takovém nálezu neposunu vzorek o jedno místo doprava, ale o nějakou hodnotu γ[0]. Pokud narazím na neshodu opět posunu vzorek, ale posun nemusí mít nutně velikost jedna jako u naivního algoritmu. Ve skutečnosti je tento posun mnohdy mnohem větší. Další odlišností je, že v případě naivního algoritmu (a vlastně i v případě Knuth-Morris-Prattova algoritmu) se zpracoval každý znak prohledávaného textu aspoň jednou (u naivního algoritmu i mnohokrát). U Boyer-Mooreova algoritmu se díky tomu, že vzorek procházím od konce, a díky tomu, že vzorek v případě neshody posunu mnohdy o více než jedno písmeno doprava, na některé znaky v prohledávaném textu vůbec nedostane (přeskočí se).
Aby se tohoto úspěchu dosáhlo, používá algoritmus dvě heuristiky (v kódu jsou reprezentovány zatím záhadnými symboly γ a λ). Jelikož jde o heuristiky dá se očekávat, že se časová složitost v nejhorším případě oproti naivnímu algoritmu příliš nezlepší. Naštěstí jsou tyto heuristiky tak efektivní a úspěšné, že v běžné praxi dosahují velmi dobrých výsledků. Jak bylo řečeno výše, spousta znaků v textu se díky těmto heuristikám může jednoduše přeskočit aniž by byly nějakým způsobem zpracovány. Na následujícím obrázku si ukážeme, jaká ja základní myšlenka obou heuristik. Jen pro zajímavost v angličtině se nazývají "bad-character heuristic" (tedy něco jako heuristika špatného znaku. Z toho se dá odvodit, že heuristika bude nějakým způsobem souviset se znakem, který v textu způsobil neshodu.) a "good-suffix heuristic" (tomu v češtině odpovídá asi heuristika dobré přípony. Opět je zjevné, že bude souviset s příponami vzorku).

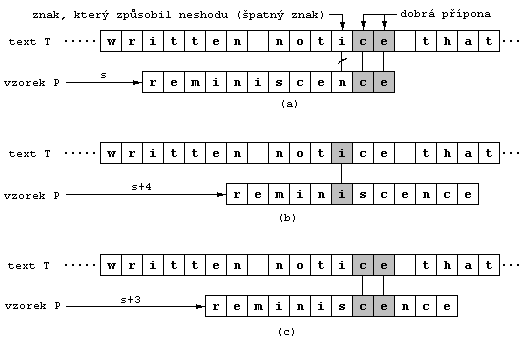
Na obrázku (a) vidíme, že hledáme vzorek reminiscence v textu T, z kterého vidíme pouze část. Daný posun s je neplatný, neboť na třetím znaku od konce došlo k neshodě (přípomínám, že se vzorek prochází odzadu). Šedě je vyznačena tzv. dobrá přípona ce. Je to část vzorku odzadu, která se shoduje s jistou částí textu, vzhledem ke kterému je vzorek zarovnán (jak uvidíme později tato část se dá velmi jednoduše určit a z ní se dá spočítat příslušný posun). Znak i, který způsobil neshodu (ve vzorku se na stejném místě vyskytuje písmeno n) je již dříve proklamovaný tzv. špatný znak.
Na obrázku (b) je načrtnuto, jak si s neshodou poradí "bad-character heuristic". Ta provede posun vzorku o tolik pozic doprava, aby špatný znak v textu byl zarovnán k nejpravějšímu výskytu stejného znaku ve vzorku. Zde je špatný znak i, a jelikož se i vyskytuje ve vzorku na sedmé pozici od konce, musím vzorek posunout o čtyři pozice doprava, aby se dosáhlo požadovaného výsledku. U této heuristiky však existují dvě výjimky. Pokud se špatný znak ve vzorku vůbec nevyskytuje, vzorek se posune o takový počet míst, aby první písmeno vzorku bylo zarovnáno k písmenu, které následuje přímo po znaku, který způsobil neshodu. V podstatě jde o nejlepší možný případ a je logické, že pokud je v textu znak, který se v daném vzorku nenachází nemusím se tou částí textu zabývat. Druhou výjimkou je, pokud je nejpravější výskyt špatného znaku napravo od aktuální pozice, kde byla odhalena neshoda (vzorek by se tedy posouval doleva). V tomto případě neposkytuje heuristika žádnou možnost.
Na obrázku (c) je zobrazeno chování "good-suffix" heuristiky v případě, že se narazí na neshodu. Tato heuristika provede posun vzorku doprava o nejmenší počet znaků, který zaručí, že znaky ve vzorku, které se po posunu budou nacházet pod dobrou příponou bude stejné jako znaky v této příponě, tedy ce. V našem příkladu je to posun o tři pozice doprava.
Když Boyer-Mooreův algoritmus narazí na neshodu, dostane v lepším případě dvě doporučení od dvou heuristik, o kolik je znaků je možno vzorek bezpečně posunout (v lepším případě, neboť heuristika "bad-character" někdy doporučení neposkytne). Algoritmus si tedy logicky vybere větší posun (v našem příkladě posun vzorku o čtyři pozice doprava).

Tuto skutečnost (míněno vybírání a vůbec užití heuristik) je v pseudokódu reflektováno na řádce (12) v případě, že byl nalezen výskyt vzorku, nebo na řádce (13) v případě, že došlo k neshodě. Zde se vybere větší číslo z j-λ[T[s+j]] (poskytnuto heuristikou "bad-character") a γ[j] (poskytnuto "good-suffix" heuristikou), o které se zvýší posun s.
Nyní se podíváme, jak jednotlivé heuristiky přesně fungují a jak se dají spočítat posuny, které poskytují. Už nyní je zřejmé, že posuny závisí pouze na vzorku, případně na abecedě Σ. Na prohledávaném textu opět příliš nezáleží.

Už bylo poznamenáno, že u této heuristiky se využívá znalost nejpravějšího výskytu znaku ve vzorku, který způsobil neshodu v textu (T[s+j]). Z toho se poté odvodí počet znaků, o který se vzorek může posunout doprava. Je zřejmé, že v nejlepším případě, kdy dojde k neshodě hned na prvním porovnávaném znaku (tedy posledním znaku vzorku) a tento špatný znak se ve vzorku nevyskytuje, je možné posunout vzorek doprava o celou jeho délku. Pokud k tomu dochází při prohledávání opakovaně, porovná se ve skutečnosti pouhý zlomek celkového počtu písmen, které prohledávaný text obsahuje. Heuristika "bad-character" tedy zajišťuje velmi výrazné urychlení vyhledávacího procesu a to i díky faktu, že porovnávání vzorku s textem se provádí zprava doleva.
Jak tedy heuristika ve skutečnosti pracuje? Nebude škodit, když k odpovědi použijeme trochu formálnějšího zápisu.
Nechť při porovnávání došlo k neshodě. To znamená, že P[j]!=T[s+j] pro nějaké j, pro které platí 1<=j<=m. Potom k buď největší číslo takové, že 1<=k<=m a zároveň P[k]==T[s+j], pokud takové k existuje. Pokud neexistuje, buď k=0. Jedná se tedy o nejpravější výskyt špatného znaku ve vzorku. Vzorek tedy můžeme bezpečně posunout o j-k znaků. V důkazu tohoto tvrzení se rozlišují tři možné případy podle velikosti k, které jsou znázorněny na následujícím obrázku.

Na obrázku (a) je ilustrován první případ, kdy se špatný znak T[s+j] (v našem příkladě je to písmeno h) ve vzorku na jiném místě vůbec nevyskytuje. Vzorek můžeme tedy bezpečně posunout o j míst aniž bychom vynechali možnost výskytu vzorku v textu (na obrázku o 11 pozic). Vzorek se zarovná pod písmeno v textu, které následuje přesně za znakem, který způsobil neshodu. Tvrzení v tomto případě platí, neboť k=0 a vzorek posuneme o j pozic, což je přesně j-k míst.
Na dalším obrázku (b) je zobrazen další případ, kdy k<j. Nejpravější výskyt špatného znaku ve vzorku je vlevo od místa j, kde došlo k neshodě. Tudíž j-k>0 a vzorek mohu o tento počet míst bezpečně přemístit doprava. Výskyt špatného znaku ve vzorku se potom zarovná ke špatnému znaku v textu. Posun je bezpečný, protože k je index nejbližšího znaku, který se shoduje se špatným, vzhledem k posunu. To znamená, že všechny posuny o velikost menší než j-k jsou neplatné a posun právě o j-k je v tuto chvíli platný (je možné, že se vyloučí hned v dalším kroku). Na obrázku máme situaci, kdy k=6 a j=10, špatný znak je i. Vzorek tedy posunu o čtyři pozice a i budou zarovnaná pod sebou.
Poslední obrázek (c) znázorňuje i poslední možnost postavení špatného znaku ve vzorku, kdy k>j. Potom by platilo, že j-k<0, což by znamenalo posunutí vzorku směrem doleva (návrat zpátky). Tato možnost se v průběhu algoritmu automaticky podchytí, neboť druhá heuristika vždy zaručí posun alespoň o jedno místo a jelikož algoritmus vybírá maximum z obou čísel, vždy se v takovémto případě vybere číslo poskytnuté heuristikou "good-suffix". V našem příkladu je špatný znak e, j=10 a k=12.

Nyní si uvedeme jednoduchý pseudokód funkce, která heuristiku "bad-character" realizuje. Funkce dostane na vstup vzorek P, jeho délku m a abecedu Σ, protože posun se musí spočítat pro každý znak, který se může vyskytnout jako špatný.

Last_Occur_func(P,m,Σ)
  (1)  for každý znak a z abecedy Σ
  (2)    λ[a]=0
  (3)  for j=1 to m
  (4)    λ[P[j]]=j
  (5)  return λ

Funkce vrací pole λ, kde λ[a] představuje pozici nejpravějšího výskytu znaku a ve vzorku a to pro všechny znaky z abecedy Σ. V případě, že se znak ve vzorku nevyskytuje je hodnota rovna nule. λ se nazývá last-occurence function čili něco jako funkce posledního výskytu.
Určení časové složitosti je jednoduché. Řádka (2) se provede tolikrát, kolik má abeceda Σ znaků, tedy |Σ|-krát. Řádka (4) se provede přesně m-krát. Časová složitost je tudíž O(|Σ|+m).

V tomto odstavci si ukážeme, jak vypočítat posuny doporučované druhou heuristikou, heuristikou "good-suffix". Pro tento účel si definujme relaci Q~R pro dva textové řetězce Q a R, pro které platí, že buď Q je příponou R nebo R je příponou Q. Tato relace neznamená nic jiného než, že pokud oba řetězce zarovnáme pod sebe podle pravého okraje, budou se ve znacích pod sebou shodovat. Zároveň platí, že Q~R právě tehdy, když R~Q.

Další vztah:
Jestliže Q je příponou R a zároveň S je příponou R, potom Q~S. Slovy řečeno to znamená, že pokud je Q příponou R a nějaké S je také příponou R, tak je jasné, že řetězce Q a S mají určitý počet znaků stejných. Tedy buď Q je příponou S nebo S je příponou Q. To je ale Q~S podle definice ~.

Nechť při porovnávání došlo k neshodě na j-tém místě vzorku (tedy P[j]!=T[s+j]), pro nějaké j<m. Potom heuristika "good-suffix" říká, že vzorek mohu bezpečně posunout o vzdálenost

  λ[j]=m-max{k: 0<=k<m & P[j+1..m]~Pk}

  λ[j]=m-max{k: π[m]<=k<m & P[j+1..m]~Pk}

Tuto definici jsme z předchozího dostali následovně.

  (1)  λ[j]=m-max{k: 0<=k<m & ...} <= m-π[m]
  (2)  π[m] <= max{k: 0<=k<m & ...}
  (3)  k >= π[m]

Úprava mezi (1) a (2) je triviální. Vztah (3) plyne z (2), neboť největší k bude vždy větší než π[m], proto takhle omezené k mohu hledat od začátku.

Pokračujme v úpravách naší nové definice λ. Z podmínky P[j+1..m]~Pk vyplývá, že buď P[j+1..m] je příponou Pk nebo Pk je příponou P[j+1..m] podle definice ~. Druhá možnost přímo implikuje, že Pk je příponou celého vzorku P (Pk je příponou P[j+1..m], což je ale přípona P. Je tedy jasné, že i Pk je příponou P). Odtud dostaneme vztah, že k<=π[m] z definice π (máme, že Pk je příponou P a zároveň π[q]=max{k: k<q & Pk je přípona Pq}. Spojením těchto dvou faktů dojdeme ke vztahu π[m]=max{k: k<m & Pk je přípona P}. Odtud plyne, že π[m]>=k, neboť π[m] se rovná maximu, tedy pro ostatní k je jistě větší.). Z této nerovnosti plyne λ[j]>=m-π[m] a to následovně.

  k <= π[m]
  m-π[m] <= m-k   pro všechna k
  m-π[m] <= m-max{k: ...}=λ[j]
  m-π[m] <= λ[j]

Definici λ můžeme dále upravit.

  λ[j]=m-max({π[m]} sjednoceno s {k: π[m]<k<m & P[j+1..m] je příponou Pk})

Odtud plyne významná skutečnost, λ[j]>0 pro všechna j (z definice plyne, že buď bude λ[j]=m-π[m] a to je určitě kladné (víme, že π[m]<m), nebo λ[j]=m-k (k je maximem z druhé množiny), v tomto případě je ale λ[j] také kladné, neboť k<m). To je věc, kterou jsme potřebovali, protože zaručí, že BM algoritmus bude posunovat vzorek stále doprava (i v případě, že první heuristika vrátí záporné číslo).
Pokračujme v naší snaze zjednodušit definici funkce λ dále. Pro další účely si zavedeme obrácený vzorek P' vzorku P a tomu odpovídající prefixovou funkci π'. Potom P'[i]=P[m-i+1] pro i=1,...,m a π'[t] je největší u takové, že u<t a zároveň P'u je příponou P't.
Nechť k je největší číslo takové, že P[j+1..m] je příponou Pk, potom π'[l]=m-j, kde l=(m-k)+(m-j).
Z toho, že P[j+1..m] je příponou Pk, plyne m-j<=k (P[j+1..m] jako přípona Pk nemůže být delší než Pk a délka P[j+1..m] je m-j) a l<=m (neboť l=(m-k)+(m-j) a předchozí nerovnost).
Také platí, že j<m a k<=m, z čehož plyne l>=1 (l=(m-k)+(m-j). První závorka je díky první nerovnosti kladná, druhá závorka je díky druhé nerovnosti nezáporná. Celé je to tedy větší nebo rovno jedné.). Jelikož 1<=l<=m je funkce π' dobře definována.
Nyní si dokážeme tvrzení π'[l]=m-j. Jelikož P[j+1..m] je příponou Pk, máme také P'm-j je příponou P'l (pouhé obrácení a přeindexování). Odtud dostaneme π'[l]>=m-j (neboť m-j vyhovuje definici π', hodnota však může být díky maximalizaci i větší.). Pro spor předpokládejme, že p>m-j, kde p=π'[l]. Podle definice π' máme, že P'p je přípona P'l. To se však dá napsat také jako P'[1..p]=P'[l-p+1..l]. Přepisem vzhledem k původnímu vzorku získáme P[m-p+1..m]=P[m-l+1..m-l+p]. Pokud teď použijeme substituci l=2m-k-j, dostaneme P[m-p+1..m]=P[k-m+j+1..k-m+j+p]. Tedy P[m-p+1..m] je přípona Pk-m+j+p. Protože p>m-j, pak j+1>m-p+1, a tedy P[j+1..m] je přípona P[m-p+1..m]. Celkem máme fakt, že P[j+1..m] je přípona Pk-m+j+p (to plyne z tranzitivity "operace suffixování" (A je přípona B a B je přípona C, potom A je příponou C)).
Protože p>m-j, máme k'>k, kde k'=k-m+j+p. Jelikož k' splňuje definici π' a dokonce k'>k, docházíme ke sporu s tím, že k je největší číslo splňující definici π'.
Tedy p=π'[l]=m-j a tvrzení je dokázáno.

Díky tvrzení máme π'[l]=m-j, z toho plyne j=m-π'[l] a dosazením do l=(m-k)+(m-j) dostaneme k=m-l+π'[l]. Díky tomu můžeme lépe přepsat definici λ.

  λ[j]=m-max({π[m]} sjednoceno s {m-l+π'[l]: 1<=l<=m & j=m-π'[l]}) =
      =min({m-π[m]} sjednoceno s {l-π'[l]: 1<=l<=m & j=m-π'[l]})

Tato definice je již natolik dobře formulována, že se dá přímo přepsat do pseudokódu. Funkce dostane na vstup vzorek P a jeho délku m.

Good_suff_func(P,m)
  (1)  π=Prefix_func(P)
  (2)  P'=Obrat(P)
  (3)  π'=Prefix_func(P')
  (4)  for j = 0 to m
  (5)    γ[j]=m-π[m]
  (6)  for l = 1 to m
  (7)    j = m-π'[l]
  (8)    if γ[j] > l-π'[l]
  (9)      then γ[j] = l-π'[l])
 (10)  return γ

Časová složitost této procedury je O(m). Časová složitost v nejhorším případě celého BM algoritmu je tedy O((n-m+1)*m+|Σ|) (složitost obou heuristik dohromady je O(m+|Σ|) a vyhledávací fáze je v podstatě naivní algoritmus). Ve skutečnosti se v běžné praxi dosahuje mnohem lepších výsledků a tento algoritmus je velmi používaný.
Postupem času se objevilo několik úprav tohoto algoritmu a dosáhlo se lineární složitosti i v nejhorším případě.

>>>Obsah

Nyní si předvedeme algoritmus, který se od předchozích liší už svým přístupem k vyhledávání v textu. Byl publikován v roce 1992 a autory jsou R. Baeza-Yates a G.H. Gonnet. Narozdíl od dvou algoritmů, které jsme si již objasnili, a kde se vyhledává pomocí porovnávání znaků ve vzorku a v textu, algoritmus BYG přišel s ideou vyhledávání pomocí bitových masek. Princip je celkem jednoduchý. I v tomto algoritmu se používá předpočítaná tabulka, nyní je to však tabulka bitových vektorů pro každý znak ze vstupní abecedy Σ. Každá bitová pozice v daném vektoru pro dané písmeno odpovídá pozici tohoto písmena ve vzorku. Z toho plyne, že každý vektor musí být tak dlouhý jako je daný vzorek. Vektor je posloupnost jedniček, ale pokud se znak odpovídající tomuto vektoru vyskytuje na k-té pozici ve vzorku, je na k-té pozici ve vektoru číslo nula.
Zde existuje několik možných variant, jak se vektory konstruují. Buď se pozice vektoru číslují odleva nebo odprava. Někdy jsou vektory nulové a výskyt znaku ve vzorku je značen jedničkou. Nejběžnější je však způsob, který jsme si ukázali a to je číslování pozic odprava a výskyt je značen nulou. Ukažme si na příkladu jak taková tabulka vektorů vypadá pro slovo states za předpokladu klasické abecedy Σ={a,b,...,z}.

Například písmeno s se ve vzorku vyskytuje na první a šesté poslední pozici, v odpovídajícím vektoru je tudíž první a šestý bit nastaven na nulu.
Na všechny tyto vektory se můžeme podívat jako na masky, kde nula je transparentní ("průhledná") a jednička netransparentní. Tyto masky potom můžeme zarovnat k danému prohledávanému textu. Uveďme si příklad. Nechť máme text misstates. Potom když k písmenům zarovnáme odpovídající masky dostaneme následující obrázek.

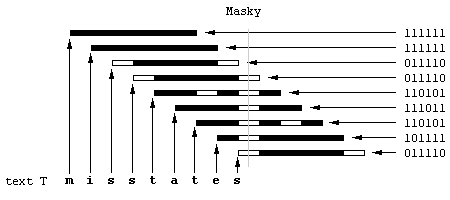
Na obrázku je každá maska zarovnána k odpovídajícímu písmenu. To znamená maska pro m je zarovnána k písmenu m v textu, maska pro i je zarovnána k i atd. Jelikož se v textu vzorek states nachází je na obrázku seřazeno šest transparentních buněk pod sebou. Šedá čára znázorňuje paprsek světla, kterým by se daly jednotlivé buňky prosvítit z jedné strany na druhou.
Abychom viděli rozdíl mezi tím, kdy se vzorek v textu najde a mezi okamžikem, kdy dojde k neshodě, ukážeme se další příklad. Tentokrát je prohledávaným textem slov mistakes.

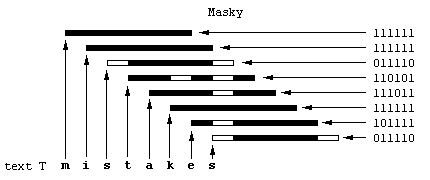
Na obrázku je vidět, že maska pro písmeno k zamezuje prosvícení bloku transparentních bitů. To znamená, že v textu se vzorek na tomto místě nenachází.
Nyní si ukážeme, jak by mohl vypadat kód pro hledání vzorku v textu algoritmem BYG (následující kód vyhledá pouze první výskyt, pro hledání všech výskytů je potřeba kód částečně upravit). Nejprve však několik poznámek. Zmíněné prosvícení buněk se v programu provádí, ovšem digitálně pomocí bitových operací. Jednotlivé masky se shromažďují v proměnné work, jejíž počáteční hodnota je -1 (v dvojkovém doplňku jsou to samé jedničky). S každým novým znakem v textu se tato proměnná posune o jeden bit doleva (vynásobí se dvěma), což odpovídá odsazování masek na obrázcích. Maska pro nový znak se k proměnné work přidá pomocí operace OR. V každém cyklu se poté tato proměnná testuje na příslušném bitu na nulovost (neboť operace OR zachovává nulovost bitů u znaků, které se shodují se vzorkem). Pokud se nula v bitu vyskytuje je vzorek nalezen, v opačném případě se pokračuje dále.
Program dostává na vstup text T a vzorek P. Nejprve se musí vytvořit tabulka bitových masek a definovat bit, který se bude testovat na nulovost (je to vlastně bit s indexem délky vzorku).

  (1)  n = length(T)
  (2)  m = length(P)
  (3)  masks = Comp_masks(P, Σ)
  (4)  testbit = 2^m
  (5)  i = 1
  (6)  found = false
  (7)  while (not found && i < n)
  (8)    while (i < n && T[i] != P[1])  i = i+1
  (9)    work = -1
 (10)    while (work != -1 && not found)
 (11)      work = (work shl 1) or masks[T[i]]
 (12)      if (work and testbit = 0)
 (13)        then found = true
 (14)             print("Vzorek byl nalezen na pozici", i+1-m)
 (15)        else i = i+1

Cyklus na řádce (8) prochází text do doby než najde počáteční znak vzorku, odtud začíná hledat vzorek podle masek. V cyklu (10)-(15) se provádí vlastní činnost, tedy posouvání a OR-ování masky spolu s testem na přítomnost vzorku.
Abychom si lépe ukázali, jak algoritmus funguje (podle kódu, který jsme se sestavili a ne podle jakési představy z předchozích obrázků), probereme další příklad. Budeme hledat vzorek state v textu misstates. Program tedy podle řádky (8) projde text až narazí na znak s, což je počáteční písmeno našeho vzorku. Potom se proměnná work nastaví na výchozí hodnotu -1. Následně se proměnná posune o jeden bit doleva (nejpravější bit bude nula) a přioruje se maska pro písmeno s. Jelikož tato maska obsahuje nulu na nejpravějším bitu, operace OR tuto hodnotu zachová. Abychom viděli, co se bude dít dál, uvedeme si tabulku. Hodnota Posun bude vyjadřovat proměnnou work posunutou o jeden bit doleva, políčko Maska představuje masku pro dané písmeno a políčko Výsledek je výsledkem operace OR na předchozí dvě hodnoty. Bit, který se testuje na nulovost je zvýrazněn.

Dále algoritmus nepokračuje, protože vzorek byl v tomto okamžiku odhalen otestováním příslušného bitu na nulu. Nyní si ukážeme obdobnou tabulku pro text, který vzorek neobsahuje, např. mistakes.

Program v tuto chvíli skončí vnitřní cyklus, neboť work=-1, což znamená, že byla nalezena neshoda. Dále by program hledal první znak vzorku (s) v textu. Nyní si ukažme jednoduchý kód, který předpočítá masky pro všechny znaky abecedy Σ. Procedura dostane na vstup vzorek P a abecedu Σ.

  (1)  for každý znak a z abecedy Σ 
  (2)    masks[a] = -1
  (3)  j = 1
  (4)  for i = 1 to m
  (5)    masks[P[i]] = masks[P[i]] and not j
  (6)    j = j shl 1
  (7)  return masks

Proměnná j slouží k vyznačování nul v příslušných vektorech. Počáteční hodnotou je jednička a s každým průběhem cyklu se hodnota zdvojnásobí (posun o jeden bit doleva). Například pokud j=4, což je v bitovém zápisu 0000000000000100. Tím, že operaci AND použijeme na masku, kterou máme, a na dvojkový doplňek j (1111111111111011), vyznačíme nulu na třetím bitu masky.
Časová složitost této procedury je O(m), protože cyklus se vykoná pro každý znak m-krát (cykly jsou sice dva, ale složitost  O(2*m) odpovídá O(m) z definice O). Časová složitost samotného vyhledávání je O(n) v nejhorším případě. Celková složitost je tedy O(n+m).

>>>Obsah

V roce 1990 publikoval člověk jménem D.M. Sunday algoritmus Quicksearch, který se od předchozích významně liší ve dvou věcech. Je rychlejší a mnohem jednodušší. Některé jeho rysy jsou podobné jako u Boyer-Mooreova algoritmu. U BM algoritmu totiž v nejlepším případě přeskočíme tolik znaků kolik je délka samotného vzorku. U Quicksearch se, jak uvidíme později, nejčastěji přeskakuje m+1 znaků (kde m je délka vzorku). Znamená to, že časová složitost v průměrném případě je méně než O(n) a blíží se k O(n/(m+1)). To je důležité zvlášť pro delší vzorky, kde je urychlení opravdu markantní. U Boyer-Mooreva algoritmu se díky tomu, že vzorek porovnáváme odzadu, v textu vracíme, což může způsobit problémy s paměťovým bufferem, které byly popsány v úvodu Knuth-Morris-Prattova algoritmu. Quicksearch nic takového nedělá, takže se jeví jako bezproblémový. Má však jiné nevýhody, které jsou popsané v další kapitole.
Myšlenka tohoto algoritmu je opravdu velice jednoduchá. Na začátku jako obvykle zarovnáme vzorek k prohledávanému textu. Stejně jako u naivního algoritmu budeme text a vzorek porovnávat znak po znaku. Postup se ale liší v případě, že objevíme neshodu mezi jednotlivými písmeny. V tomto okamžiku se podíváme na znak, který se nachází v textu přímo za koncem vzorku (testový znak). Pokud se tento znak ve vzorku na žádném místě neobjevuje, žádný posun, který by umístil jakékoli písmeno vzorku nad testový znak, nebude platný. S klidným svědomím tedy můžeme celý vzorek přemístit až za testový znak. To představuje posun o m+1 znaků, kde m je velikost vzorku. Tato vzdálenost je mnohem lepší než v případě předchozích algoritmů (včetně BM algoritmu, kde byl posun v tomto případě pouze m).
Pokud se testový znak ve vzorku na nějakém místě nachází (případně na více místech), posuneme vzorek o nejmenší vzdálenost takovou, že se testový znak bude shodovat se znakem v nově posunutém vzorku, který je zarovnán k testovému znaku. Většinou to bude představovat posun o více než jeden znak. Dalším porovnáním zjistíme, jestli byl posun spravný a vzorek se na této pozici již nachází. Jinak se posuneme stejným způsobem dále. Pro lepší ilustraci, jak tento algoritmus v textu vyhledává, si uvedeme příklad. V následujícím textu budeme hledt výskyt vzorku problems.

Na obrázku (a) je vyobrazena výchozí situace. Hned první znak textu způsobuje neshodu. Testový znak je písmeno h. Jelikož se takové písmeno ve vzorku nevyskytuje, posuneme vzorek o jeho délku zvětšenou o jedna (tedy o devět znaků). To znamená, že se vzorek posune až za písmeno h.
Situace je ilustrována na obrázku (b). Tentokrát je testový znak písmeno e, které se ve vzorku vyskytuje. Proto musíme vzorek posunout tak, aby byly dvě e zarovnány pod sebe. Tato vzdálenost musí být o jednu větší než je e vzdáleno od konce vzorku. Vzorek tedy posuneme o 8-6+1=3 znaky.
Na obrázku (c) opět došlo k neshodě na prvním porovnávaném znaku. Testový znak je prázdné políčko, které se ve vzorku nevyskytuje. Znovu posuneme vzorek o devět míst.
Následuje situace z obrázku (d). Zde se stejně jako u naivního algoritmu porovnají tři znaky (pro). Na čtvrtém písmenu dojde k neshodě. Protože testový znak i se ve vzorku nevyskytuje, přemístíme vzorek až za tento testový znak, tedy opět o devět míst.
Obrázek (e). Zde je opět testovým znakem písmeno e a stejně jako v případě (b), posuneme vzorek o devět míst.
Na obrázku (f) je zobrazena konečná situace. Vzorek je nalezen a bylo k tomu potřeba pouhých pět posunů a celkem 16 porovnání.

Nyní se už můžeme uvést jak bude algoritmus vypadat zapsán v pseudokódu. Na vstup procedura dostane text T, vzorek P a abecedu Σ. Procedura opět vyhledá pouze první výskyt pro nalezení všech výskytů jsou však třeba jen drobné úpravy. Tabulku posunů shift je nutno před samotným vyhledáváním předpočítat.

  (1)  n = length(T)
  (2)  m = length(P)
  (3)  shift = Comp_shift(P,Σ)
  (4)  pat = 1
  (5)  s = 0
  (6)  while (pat <= m && pat+s <= n)
  (7)    if P[pat] == T[pat+s] 
  (8)      then pat = pat+1
  (9)      else s = s+shift[T[s+m+1]]
 (10)           pat = 1

Comp_shift(P,Σ)
  (1)  for každý znak a z abecedy Σ
  (2)    shift[a] = m+1
  (3)  for i = 1 to m
  (4)    shift[P[i]] = m-i+1
  (5)  return shift

Kód je pouze přepisem faktů, které tu byly vysvětleny. Snad jen poznámka k funkci Comp_shift. V prvním cyklu se všem znakům přiřadí hodnota maximálního posunu a teprve poté se provádí pro znaky, které se ve vzorku vyskytují, přesnější úprava.
V nejlepším případě se neshoda objeví pokaždé hned u prvního porovnávaného znaku (u prvního myšleno jako prvního po každém posunu). To znamená, že posun bude pokaždé o m+1 znaků. Časová složitost je potom asi O(n/(m+1)). Kompletní analýza časové složitosti tohoto algoritmu zatím nebyla poskytnuta, ale Sunday tvrdí, že není horší než O(n).

>>>Obsah

V této kapitole si řekneme výhody a nevýhody algoritmů, které zde byly popsány. Na jaké účely se hodí a na jaké ne.
První algoritmus, kterému jsme se věnovali, byl tzv. naivní algoritmus (odkaz). Myslím, že nemá cenu se tomuto algoritmu věnovat moc dlouho, neboť svou časovou složitostí není předurčen k příliš velkému použití. Na druhou stranu pro relativně krátké texty (řádově o stovkách maximálně tisících znacích) a krátké vzorky (20 písmen) je tento algoritmus asi dobrou volbou, a to už jenom z důvodu, že ostatní efektivní algoritmy si pro své potřeby předpočítávají různé tabulky, což tento algoritmus nedělá, a proto se u krátkých textů jeho pomalost neprojeví a vzhledem ke své jednoduchosti implementace je mnohdy používán (implementace v assembleru, použití v jednoduchých textových editorech apod.). Jeho nevýhodou je, že při použití pro vyhledávání v souborech může dojít k problému s paměťovým bufferem, který je popsán v úvodu kapitoly věnované Knuth-Morris-Prattovu algoritmu.
Dalším algoritmem, který jsme si ukazovali, je právě Knuth-Morris-Prattův algoritmus (odkaz). Tento algoritmus odstraňuje hlavní nevýhody naivního algoritmu. Je to především vícenásobné testování jednoho znaku a vracení se v textu. Díky tomu je vhodný pro vyhledávání v textových souborech, neboť nevznikají problémy s paměťovým bufferem (pravděpodobnost, že se tento problém vyskytne, je sice malá, ale přihodit se může). Nevýhodou ale je, že se stále porovnávají všechny znaky textu (i když jak uvidíme později, pro jisté speciální účely je to nezbytné). Algoritmus se hodí pro vyhledávání vzorků, o kterých nejsou k dispozici žádné informace, a tedy není jisté, jestli by bylo výhodnější použít obyčejný naivní algoritmus.
V další kapitole jsme se věnovali algoritmu Boyera a Moorea (odkaz). Tento algoritmus je asi všeobecně nejlépe použitelný i přes svou relativní složitost implementace. Je zvláště vhodný pro vzorky větší délky a pro relativně velkou abecedu znaků, kde se obě heuristiky mohou plně uplatnit. Narozdíl od předchozích algoritmů, tento prozkoumá pouze zlomek všech znaků v textu (to se ale v některých případech může nevyplatit). Bohužel díky zpětnému porovnávání vzorku s textem může dojít stejně jako u naivního algoritmu k problémům s paměťovým bufferem, který vyžaduje další režii výpočtu. I přes nepříliš dobrou časovou složitost je v průměru velmi dobrý.
Následuje algoritmus Baeza-Yates-Gonnet (odkaz). Tento algoritmus je velmi specifický, a proto jsou s ním spjatá i jistá omezení co do implementace. Prvním omezením je požadavek na schopnost programovacího jazyka (a počítače) provádět bitové operace OR, AND a bitový posun, na číslech typu integer. Druhým a po pravdě řečeno asi drastičtějším omezením je délka bitových masek, které se v algoritmu používají. Tyto masky musí mít stejnou délku jako daný vzorek. Dnešní počítače počítají vše buď v 32-bitové nebo v 64-bitové aritmetice, což je omezení pro kompilátory programovacích jazyků a tím i pro délku bitové masky. Proto v případě, že chceme hledat vzorek delší než 32 (potažmo 64) bitů, není tento algoritmus i přes svou rychlost tou správnou volbou. Na druhou stranu, pokud chceme sestrojit algoritmus, který nebude case-sensitive (tedy nebude rozlišovat velikost písmen), není problém upravit Baeza-Yates-Gonnetův algoritmus tak, aby tento požadavek bez problémů řešil. Stačí pouze vyrobit masky zvlášť pro velká a malá písmena a trochu upravit vyhledávací část.
Tím se dostáváme k poslednímu algoritmu, který zde byl popsán, Quicksearch (odkaz). Nejdříve dvě fakta. Za prvé tento algoritmus se stejně jako KMP a BYG v textu nevrací zpět. Za druhé, stejně jako Boyer-Mooreův algoritmus i tento přeskakuje velké množství neporovnaných znaků. Jak bylo řečeno, je tato skutečnost výhodou co do urychlení algoritmu, ale ve speciálních případech není toto přeskakování žádoucí. Takovým příkladem může být situace, kdy při každém nalezení vzorku v textu chceme, aby program nahlásil číslo řádky, kde se vzorek vyskytuje. V případě, kdy program počítá každý znak pro novou řádku a tento znak se posunutím vzorku o několik pozic přeskočí, dochází při nahlášení výskytu vzorku ke zkreslení informace o čísle řádky. Proto je při výběru algoritmu nutné uvažovat, k čemu bude sloužit. Testy ukázaly (na textech o délce přibližně 200000 znaků), že Quicksearch si velmi dobře počíná v situacích, kdy je vzorek relativně delší. Při nejčastějších délkách vzorků (od šesti do osmi písmen) porovná algoritmus pouze přibližně jednu šestinu všech znaků. Záleží však i na tom, jak vzorek vypadá. Existují dvě upravené verze (maximal shift algorithm a optimal shift algorithm), které dosahují o pět procent lepších výsledků než základní algoritmus. Vzhledem k tomu, že před vlastním vyhledáváním předpočítávají spoustu různých věcí, jsou ale vhodné pouze pro texty délky řádově o stotísících znacích.

>>>Obsah

V tomto dokumentu jsme popsali několik algoritmů zabývajících se vyhledáváním vzorků v textu. Všechny mají jednu vlastnost společnou, vyhledávají jeden vzorek v textu. Samozřejmě existují i algoritmy, které vyhledávají celé množiny vzorků (algoritmus Aho-Corasickové, algoritmus Commentz-Walterové) i množiny zadané pomocí regulárních výrazů (B-algoritmus). I přesto jsou tyto algoritmy velice užitečné a svou vzájemnou rozdílností je spektrum jejich použitelnosti poměrně široké. Dále jsme si uvedli výhody a nevýhody jednotlivých algoritmů, k čemu se hodí a k čemu. U každého je vedle podrobného vysvětlení i pseudokód, podle kterého by neměl být problém daný algoritmus naprogramovat.
Tento dokument je tedy jakýsi úvod do problematiky vyhledávání v textu, neboť tato úloha je velice rozsáhlá a zasahuje do mnoha oborů teoretické informatiky.

>>>Obsah

Zde jsou uvedeny použité materiály.

• T.H.Cormen, C.E.Leiserson, R.L.Rivest: Introduction to Algorithms, MIT Press 1990, kapitola 34 - String matching
• Ivana Vovsová: Vyhledávání vzorků v textu, diplomová práce, MFF 1994
• String Searching, článek z neznámé knihy od neznámého autora
• A. Koubková, J. Pavelka: Úvod do teoretické informatiky, MFFPress 1998

>>>Obsah